Twin Primes
Definition
Twin primes are pairs of primes which differ by two. The first twin primes are (3,5), (5,7), (11,13) and (17,19). It has been conjectured, but not proven to date, that there are infinitely many twin primes.
Twin primes become increasingly rare as higher numbers are examined, in keeping with the general tendency of gaps between adjacent primes to become larger as the numbers themselves get larger. However, it is a long standing conjecture that there are infinitely many twin primes.
Twin Prime Conjecture
It is conjectured that there are infinitely many twin primes and while testing suggests that this is true, a theory to support this notion has yet to be discovered.
Facts and Theories
Every twin prime pair except (3, 5) is of the form (6n − 1, 6n + 1). That is the twin prime pair of 17,19 is of the form (6x3-1, 6x3+1).
Usually the pair (2, 3) is not considered to be a twin prime. Since 2 is the only even prime, this pair is the only pair of prime numbers that differ by one and is therefore excluded from the scope of twin primes.
Beginning in 2007, two distributed computing projects, Twin Prime Search and PrimeGrid, have produced several record-largest twin primes. As of January 2016, the current largest twin prime pair known is 3756801695685 · 2666669 ± 1,[15] with 200700 decimal digits. It was discovered in late 2011. You can join the search by enrolling in PRIME Grid to search for twin primeshere...
Frequency of Twin Primes
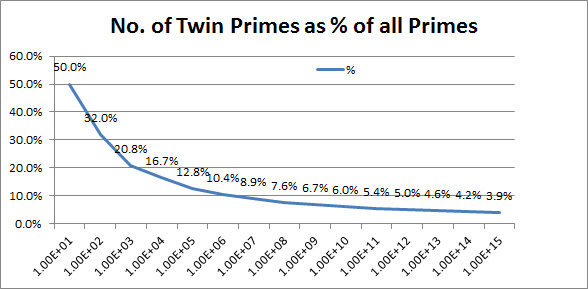
The following table gives you an insight into the frequency of twin primes. You can see that the ratio of twin primes as a proportion of all primes decreases.
For example if you take all numbers less than 1,000,000 there are 50,847534 primes but only 6.7% (3,424,506) of these primes are twin primes. Note this graph only counts the first number in a twin prime pair.
Twin Primes Finder
If you want to find twin primes I have included a twin prim calculator here...
